In a couple of my timeline posts at the end of last week, I mentioned an annual competition on Hum in the Fochrik system, the homeworld of the Humma race in Star Frontiers. The tweets were as follows:
FY60.032 – Contestants, spectators, and reporters gather on Hum (Fochrik) for the annual Humma Jump Competition. Speculation is high that the current record in the standing long jump event of 38.272 meters will be surpassed this year. #SFTimeline
— Star Frontiers RPG (@StarFrontiers) February 7, 2019
FY60.034 – After two days of competition, Zonuul Usu of Larg (Fochrik) wins the Humma Jump Competition jumping 38.275m, beating the previous species record by 3 millimeters. Two others beat the previous record in the final round of competition but lost to Zonuul. #SFTimeline
— Star Frontiers RPG (@StarFrontiers) February 9, 2019
This immediately got me thinking about how the Hum calendar interacts with the Galactic Standard calendar of the Frontier and if the Rim had a different standard calendar.
Since in my Clarion calendar system post, I mentioned that I would probably do more calendar systems for other planets and in my last State of the Frontier post I said I would write about creating a system map, I thought I’d roll all of these thoughts and ideas into a series of “how to” posts as I flesh out the Fochrik system.
I’m planning on dividing this into three parts. In this first article, I’ll be talking about generating the astrophysical description of the system. We’ll go over what we know from published material, adding a bit to that, refining the details, and trying to generate a stable star system.
In the next post, I’ll actually walk you through the process of creating a system map for Fochrik like I did for the Duergan’s Star system.
In the third post, I’ll generate a calendar for the Fochrick system. I don’t know yet if all three planets will have a unique calendar or if Larg and Forge will base their calendar off of Hum’s. We’ll see when we get there. I’m not planning to address a standard Rim calendar at this time as I need to look over the other Rim systems first. That may be a future post.
Anyway, let’s get started.
What We Know
Let’s start with what we know from published materials, both original with TSR and material from the fan magazines. There isn’t much, but let’s assemble what we have.
The Rim was introduced in TSR’s Zebulon’s Guide to Frontier Space, vol 1 as the area of space that the three new races introduced came from. It was specifically left vague in the supplement. Whether they intended to flesh it out more in later volumes that never were published we’ll never know. On page 50, in the “Planets of the Frontier” table we have the following entry for Fochrik:
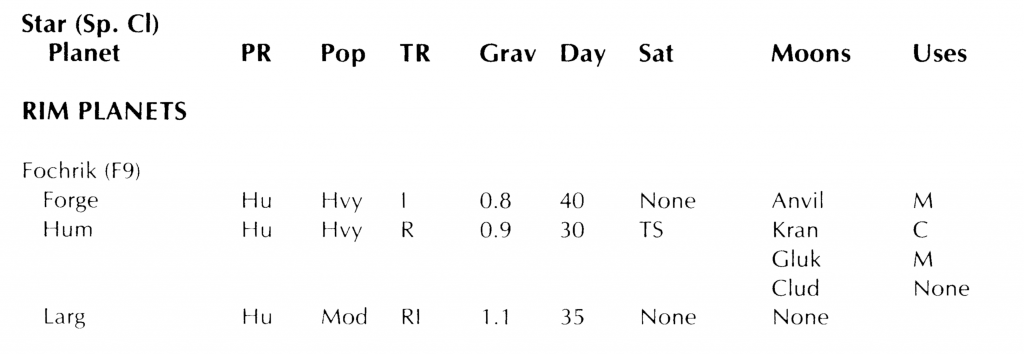
For this series of posts, we’re interested in the stellar spectral type (F9), the number of known planets (three in this case) and their rotational period (the Day column which is given in hours). Also, the number of moons might be used in making the system map and we should probably consider them in making the calendars as well. The other information is not needed for this endeavor.
Beyond that, there is little said about the system in Zeb’s Guide. The worlds of the Frontier have little blurbs with interesting facts about each of them but there is nothing on any of the Rim worlds. We’re basically left with a blank slate.
In a Star Frontiersman article (issue 15), entitled Humma Hop Back, TheWebtroll talked about the race but gave no information on the star system. Tom Verrault did a little bit of work on the Humma in issue 13 of the Frontier Explorer were he fleshed out their racial description some more but again nothing was really mentioned about their star system. However in another article in that same issue, where he adds detail to the boon’sheh, a fan created race from the early Star Frontiersman issues, he places them with the humma in the Fochrik system with the humma forcibly relocating the boon’sheh to Larg from their mutual homeworld of Hum. But that’s all we have.
In the end, we just have the table entry for the system to work with. Which tells us we have three habitable planets, some moons, and their approximate rotation periods. We get to create everything else so let’s dive in.
Fochrik
We start with the star. It is given a spectral type of F9. That makes it a little more massive and brighter than the sun but not by much. I like to use the table on this page for my starting point of stellar masses and radii as it has broken the data down in to details for each spectral classification. Plus the author has gone through, and based on the spectral energy distribution, given you the RGB colors for the star. I’m a little leery of the radius data on that page but we won’t be using that in this analysis.
From that page we get a mass of the F9 star for 1.1 solar masses. Looking at the adjacent spectral types, F9 and G0, they have listed masses of 1.2 and 1.1 respectively so that gives us a range to work with and tells us that the F9 star is probably a bit heavier than 1.1 solar masses but within rounding errors. Plus there is scatter based on other factors as well so we have some room to wiggle about. Let’s do some quick calculations.
The mass of the sun is 1.989 × 1030 kg. so we have a range of 1.1 to 1.2 times that to work with or from 2.1879 × 1030 to 2.3868 × 1030 kg. Like I did for White Light, I want a few more decimal places so I’m going to roll some dice for the digits. I’ll keep the 2 before the decimal place, roll a d4 for the first digit, and then d10s for everything else. That will possibly let me go slightly outside the range but that’s fine. Here’s what we get:

So we end up with a stellar mass of 2.21766549 × 1030 kg which probably has more decimal places than we need but that’s fine.
Size of the Habitable Zone
The next thing we need to know is the range of the habitable zone for an F9 star. We’ve got to squeeze three planets into that area. We don’t need to be exact, but we want some reference. For this Wikipedia has a good article on the habitable zone that you can read to determine the various factors that go into determining it. There is also a really great picture (reproduced here) that almost gives us what we need.

The only real problem with this image is that the x-axis is in relative flux on the planet rather than distance. But I can work with that to get values for Fochrik.
We start by getting the percentages for the edges of the habitable zones. This is done by drawing a line across at the temperature of Fochrik (6140 K) and then drawing lines down from those to the x axis like this (the blue lines)
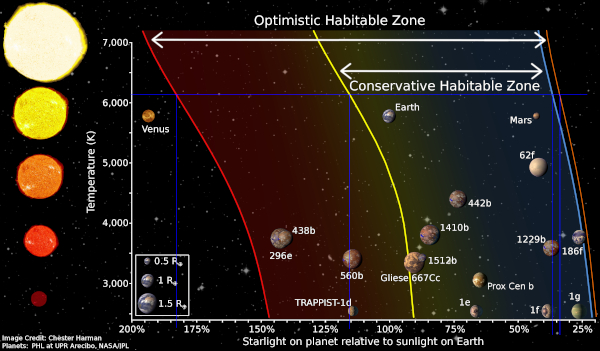
This gives us a range of 178% to 34% for the optimistic habitable zone and a range of 115% to 36% for the conservative one. Now we just need to turn those into distances.
The amount of starlight on the planet is dependent on three things. The first is the temperature of the star (which we’re taking to be 6140K. We could figure it out exactly based on the mass but that is a close enough approximation). The second is the radius of the star. These two give us the total luminosity of the star, L, which is proportional to R2T4. The final bit, which we are trying to solve for, is the distance from the star. The amount of starlight received at a planet, F (flux), is proportional to the luminosity of the star divided by the distance squared, i.e. F~L/D2.
Combining those gives us that the amount of starlight at a planet, F, is proportional to R2T4 / D2. or D ~ sqrt(R2T4 / F). If we work in ratios to the solar temperature, solar radius, measure distances in AU (the distance from the earth to the sun), and enter fluxes as multiples of the flux at the earth (i.e. flux at earth =1, 200% = 2, 50% = 0.5, etc), everything works out.
For this exercise, we’re going to assume the radius of the star is the same as the sun. In reality, it’s probably a little bit larger but we’re not going to worry about that. So we can drop the R2 term. The ratio of the temperatures is just 6140/5780 = 1.062283737. That raised to the 4th power is 1.273392. Plugging in those number gives the following distances for the four flux percentages:
- 178% = 0.8458 AU (inner edge of optimistic habitable zone)
- 115% = 1.0523 AU (inner edge of conservative habitable zone)
- 36% = 1.8807 AU (outer edge of conservative habitable zone)
- 34% = 1.9353 AU (outer edge of optimistic habitable zone)
Those numbers seem about right. The star is brighter and hotter than the Sun so it makes sense that the habitable zone is a little further out than in the solar system.
Placing the Planets
Now that we know where the habitable zone is, we need to place the planets and add other details to the system. We start with the three known planets, Forge, Hum, and Larg.
The Habitable Worlds
Each of these planets is habitable, with fairly large populations. As such, they need to be at least somewhere within the habitable zone. Also, since they are relatively low gravity worlds, around 1g, they should probably be close to or in the conservative habitable zone as the optimistic one is more for “super earths” which these are not.
Forge is the innermost world of the three and the name itself implies that it’s a hot world. I’m going to place it just inside the conservative zone. It’s livable, but its a bit on the warm side. We’ll place it at 1.08 AU from Fochrik.
Hum is the humma homeworld. As such we’d expect it to have a relatively nice, comfortable climate. If we go back to the flux calculation from above and find the distance for 100% we get a distance of 1.13 AU. That’s a little too close to the 1.08 AU I picked for Forge so I’m going to move it out just a bit further than that and place it at 1.23 AU. It will be a bit cooler than Earth receiving only 84% the amount of starlight.
Finally, we have Larg. This has the smallest population, medium instead of heavy, so I’m taking that to mean that it probably has a less hospitable climate (in addition to the higher gravity). Plus, if we’re using the fan material from the Frontier Explorer, it’s where the humma deported the boon’sheh to. We’ll place this one out towards the outer edge of the conservative habitable zone at 1.61 AU.
Now that our habitable planets have been placed we need to fill the rest of the system. There are a number of ways you could do this. I have a really old program called StarGen that makes solar systems around F, G, & K type stars based on habitability ideas presented in a paper by the Rand corporation. It works pretty well but doesn’t take into account modern information as that paper is from the 60’s or 70’s if I remember correctly.
You could also use the star system creation system presented in the FrontierSpace Referee’s handbook. It’s a good system as well. However, for this system I’m just going to be arbitrary. I’ll roll some dice for distances but beyond that, I’m just going to pick what I want in the system.
The Inner Worlds
Let’s start close. What is inside the habitable planets? I’m going to place two small worlds in there. They are small, hot, and airless. They probably have mineable mineral resources but they are not very hospitable. We’ll place these worlds at .19 AU and 0.52 AU from Fochrick. To get those distances I simply rolled 4d10 and 9d10 respectively and divided the number by 100 to get the AU.
The Outer Worlds
Next let’s move out from the inner system and see what’s out in the outer reaches. We’re going to add in 6 more worlds outside the habitable zone. For now, I’m not planning on having an asteroid belt but that may change when we do some sanity checks below. We’re going to add the following planets to the system:
- Jovian – 4.66 AU
- Jovian – 10.59 AU
- Ice dwarf – 16.58 AU
- Ice giant – 18.13 AU
- Ice dwarf – 20.53 AU
- Ice giant – 26.01 AU
In each of these cases, to get the distance I created a number between 1 and 6.99 by rolling a d6 and two d10s. The d6 was the integer bit and the two d10s were the decimal bit. I then added that number on to the orbital distance of the previous planet. Like I said, this was going to be pretty arbitrary. Let’s keep going.
Orbital Periods
Now that the planets are all placed, we want to compute their orbital periods to know how long the length of their orbit is. While we don’t need this to create the map of the system. We want to do some sanity checks since the planetary placements were fairly arbitrary.
Orbital periods are given by Newton’s form of Kepler’s Third Law of Planetary motion, namely:

which I described in the Clarion Calendar post but P is the orbital period, a is the distance from the star, G is the gravitational constant, and M1 and M2 are the mass of the star and planet respectively. Since M1 >> M2, we’ll ignore M2 in our calculations.
You could do this by hand, or use a spreadsheet, or use an on-line calculator. I’m going to use this handy website that allows you to enter the values in a number of different units and does the math for you. I’m just going to leave the mass of the planet at 1 earth mass in the calculation. If I was going for full detail, I’d figure out the mass of each of the planets but this is really just an approximate sanity check. For example, if I set the mass of the first Jovian planet to 100 earth masses, it would lengthen the orbital period by only 10 hours, so it’s not something I’m going to worry about here.
Plugging in the values for the planetary orbital distance and the mass of the star we get the following data:
| Planet | Orbital Distance (AU) | Orbital Period (hours) |
| T1 | 0.19 | 687.46 |
| T2 | 0.52 | 3112.57 |
| Forge | 1.13 | 9316.45 |
| Hum | 1.23 | 11323.3 |
| Larg | 1.61 | 16957.2 |
| J1 | 4.66 | 83501.4 |
| J2 | 10.59 | 286061 |
| ID1 | 16.58 | 560391 |
| IG1 | 18.53 | 662106 |
| ID2 | 20.53 | 772144 |
| IG1 | 26.01 | 1101096 |
Mainly here I’m just looking to see that we don’t have any resonant periods with the two Jovian planets. With orbital periods in ratios such as 2:1, 3:2, & 3:1 we would have potential stability issues. My only concern is with the second jovian and the first ice dwarf. They are in a nearly 2:1 orbital resonance but that might actually be okay and why that planet is where it is. So I’m going to leave it alone. If I really wanted to check system stability, I’d generate the masses, starting positions and velocities, and then enter all of that into a simple n-body computer simulation and run it for a million years or so of simulated time to make sure nothing went crazy but I think this will be fine.
Planetary Sizes
Okay, while this isn’t strictly necessary to draw the system map, we might as well figure out how big each of the planets are (and their surface gravity. When I do the system map, I like to have both the distances to scale and the sizes of the planets to scale so if I want to do that, I need the sizes.
The equation we’ll be using for this is
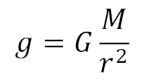
where g is the acceleration due to gravity (m/s2), M is the mass of the planet (kg), r is the radius of the planet (m), and G is just the gravitational constant (6.67408 × 10-11 m3 kg-1 s-2). Additionally we’ll want an equation relating the mass of the planet to its density which is just the volume of the sphere times the density or
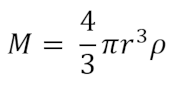
where ρ is the density (kg/m3). While we could do this just with the mass, I like to make sure the physics work out for the type of planet so I like the densities to make sense and prefer to include it in the calculations. Combining those two equations gives us an equation that relates the gravity, the radius, and the density:
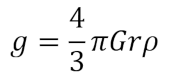
This is what we’ll be using to get the data we need.
Densities
As part of this we’ll need densities for the planets. We’ll just be picking those from reasonable ranges which are the following (in g/cm3):
- Terrestrial (rocky) Planets – 3.5 – 5.7
- Ice Dwarfs – 1.8 – 2.5
- Ice Giants – 1.2 – 1.8
- Jovians – 0.6 – 1.4+
To get it into the units we need (kg/m3 ) we just multiply by 1000. The Jovian planets may not have an upper density limit because once you get to be the size of Jupiter, adding more mass doesn’t change the radius much, it just increases the densities. Brown Dwarfs, which are 10-80 times Jupiter’s mass are still all about the same size.
We’ll use these density ranges to pick densities for the individual planets in the sections below.
The Habitable Planets
First up are the three habitable planets that we know the gravity on. In this case we need to rearrange the last equation to solve for r giving us:
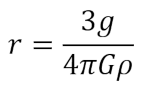
All that’s left is to pick a density or each of the planets and start computing. Well, almost. I also want one more decimal place for the actual gravity of the planet. To get that I’ll roll d8-4 x 0.01 and add that to listed gravity to give me some variation that would round to the listed value.
The table below is what we ended up with. Interestingly, all the gravity adjustments I rolled were positive. I also selected the planets with the higher gravity to be a little more dense but modulated that somewhat due to the fact that planets that form closer to the star would have higher density as well. Thus the densities of these three planets are pretty close together.
| Name | Gravity (g) | Density (gm/cm3) | Mass (Earth) | Radius (km) |
| Forge | 0.81 | 5.32 | 0.6012 | 5,443.75 |
| Hum | 0.91 | 5.43 | 0.8139 | 5,991.93 |
| Larg | 1.12 | 5.55 | 1.4622 | 7,215.22 |
Hum turns out to be almost exactly the same size and mass as Venus, just a little further out in the system so it’s not as hot. Forge is smaller still by about 10% in radius and 75% in mass while Larg is about 13% larger in radius than the earth and almost 50% more massive.
Other Planets
Now lets due the rest of the planets in the system. In this case we have to pick two of the three values: radius, density (or mass), and surface gravity. I’m going to select the radius and density for each of these planets and then compute the mass and surface gravity. Surface gravity doesn’t exactly make sense for the giant planets (jovians and ice giants) but it is the gravity present if you were stopped at that radius at it’s upper atmosphere. Here’s the table:
| Name | Gravity (g) | Density (gm/cm3) | Mass (Earth) | Radius (km) |
| T1 | 0.33 | 5.65 | 0.0349 | 2,064.55 |
| T2 | 0.67 | 5.39 | 0.3373 | 4,468.50 |
| J1 | 3.30 | 1.48 | 525.82 | 79,714.14 |
| J2 | 1.55 | 0.92 | 140.14 | 60,108.51 |
| ID1 | 0.14 | 2.22 | 0.0189 | 2,297.74 |
| IG1 | 0.97 | 1.21 | 19.902 | 28,623.16 |
| ID2 | 0.06 | 2.19 | 0.0018 | 1054.47 |
| IG2 | 1.02 | 1.35 | 18.472 | 26,919.75 |
J1 is almost two times the mass of Jupiter while IG2 is a little smaller than Pluto. If you want to compare them exactly this Planetary Fact Sheet page gives the data for all the planets in the solar system.
Wrapping up for now
And that’s it for this entry. We have the number of planets in the system, mass data on the star, and orbital and size data on the planets. I’m fairly confident that we don’t have to worry about system stability issues (of course since I didn’t do a rigorous check, this will be the one time it doesn’t work 
In the next post, we’ll create a system map for Fochrik and walk through the process of doing so. If you have any questions or comments, let me know below.