With work on the next issue of the Frontier Explorer happening, it’s taking me a bit longer to get to these posts than I had hopped but progress is being made. And I haven’t yet fallen behind.
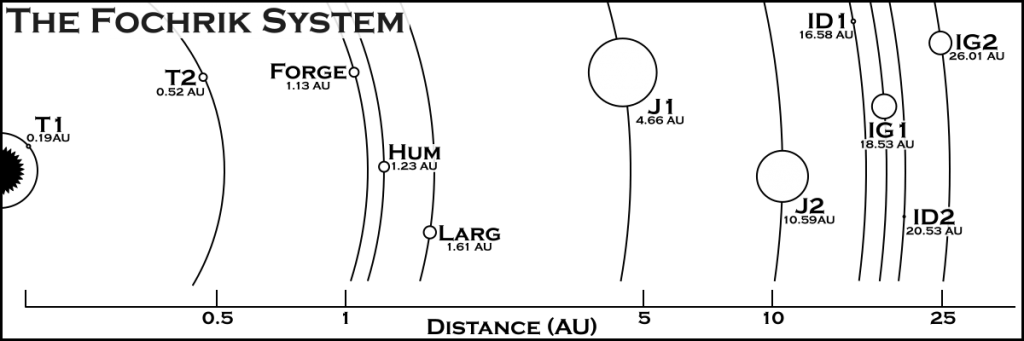
Today we build the calendar system for Hum, the humma homeworld in the Fochrik system, which we have been detailing in the previous posts (part 1, part 2) in this series.
The Data

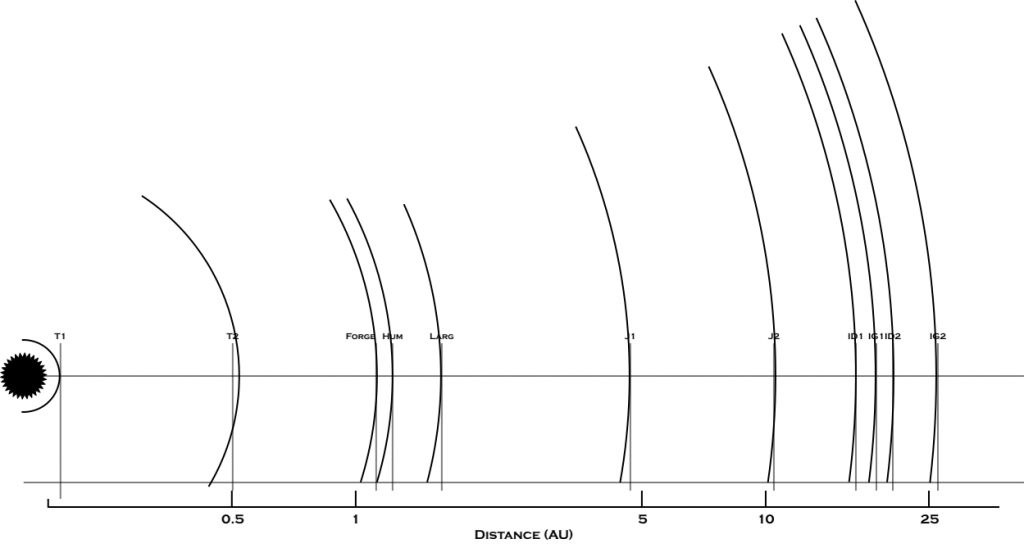
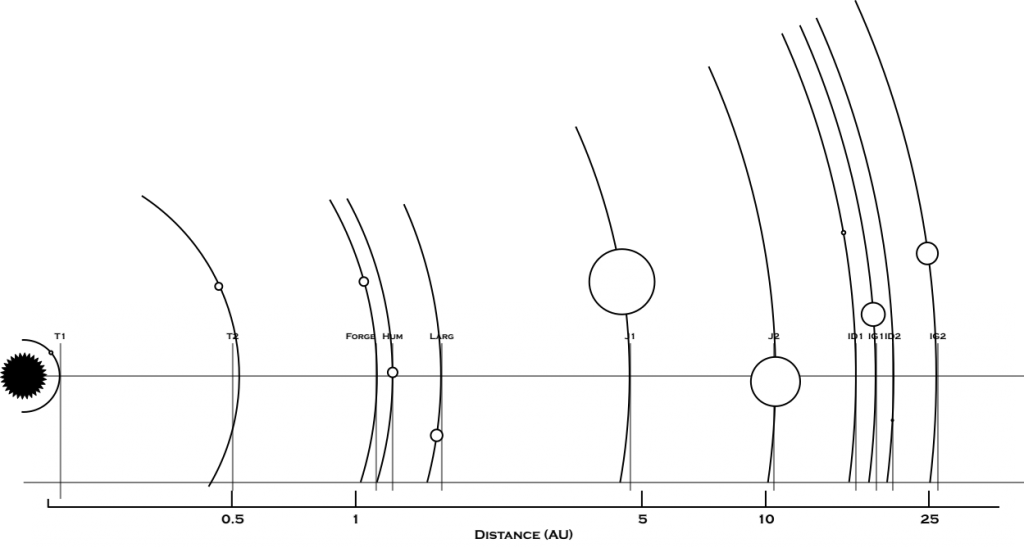
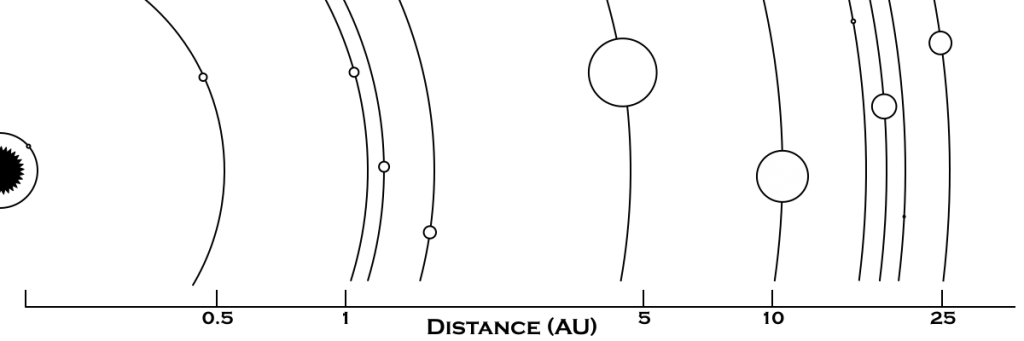
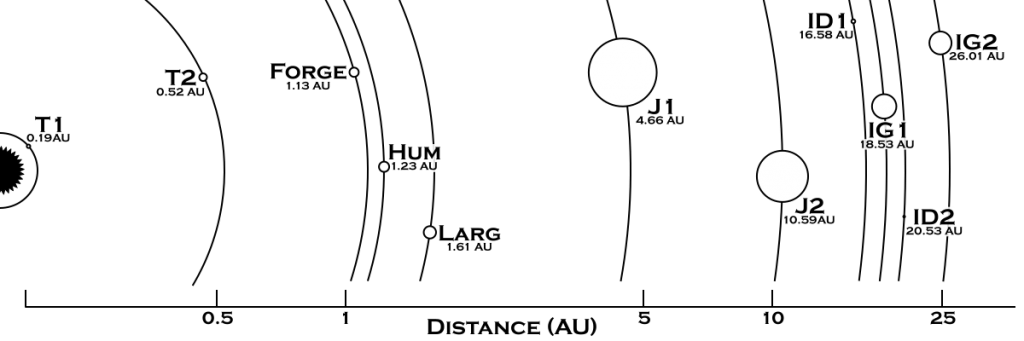
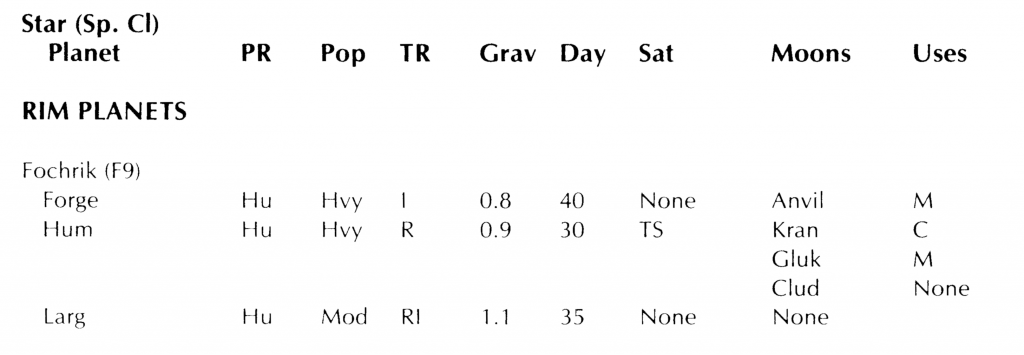
In the first part of this series, we established the following facts about Hum:
- From Zebulon’s Guide to Frontier Space
- Rotational period: 30 hours (we’re going to refine this a bit later on)
- Surface gravity: 0.9g (which we increased the precision on to 0.91g)
- 3 moons: Kran, Gluk, & Clud
- From our calculations:
- Orbital Distance: 1.23 AU
- Orbital Period: 11323.3 hours
- Density: 5.43 gm/cm3
- Mass: 0.8139 Earth masses
- Radius: 5,991.93 km
Of those parameters, we won’t be using the surface gravity, radius, or orbital distance in this analysis but we will be using the rest.
The Moons
I ignored the moons in the early parts of this series but now they become important so we need to detail them out a little bit more. Just as the orbital period of the Earth’s moon defines the concept of a month for us, given that this is the humma homeworld, the orbital periods of Hum’s moons would probably play a roll in defining their calendar system as well. So lets figure out the data on Hum’s moons.
All we really have to start with is the fact that there are three moons and their order (assuming the first one listed is the closest). Beyond that, we can really do whatever we want. That said, we have a few considerations to keep in mind.
First, Hum is smaller than Earth (about the size of Venus) and so has a smaller gravitational pull. This just means that the larger the moon, the more it will cause the planet to “wobble” about their common center of gravity. So we may not want any moon to be too big. It also means that if the moons have to be too far away, they might have escaped the planet’s gravity well. This latter point shouldn’t be an issue but is something to keep in mind.
Second, the moons will all mutually interact gravitationally. Which means if we have strong orbital resonances (orbital periods in small integer ratios), or if they have very close passes (with “close” depending on their relative sizes) as they orbit, the moon system may be unstable and not have survived to the present day.
So while we can pick anything we want, we should keep those ideas in mind. Now ideally, after picking the parameters for the moons and their orbits, I would generate orbital data for them all and run them through several hundred thousand or several million years of orbits to confirm stability but I didn’t do that. So we’ll just hope what we come up with something that makes sense and works.
The other thing to consider is what role we want to attribute to the moons in regards to the calendar system. This will have an impact on the orbital periods we pick.
Kran
Kran is the innermost moon of the system. It will have the shortest orbital period of the three. As such, I decided that this moon would also be the smallest and associated with the “week” concept on Hum.
Since I want the “week” to be something on the order of 5 to 10 local days, and as I have no real reason to prefer one value of another, I’ll just roll 1d6+4 to get the value. I rolled a 5 so a Hum week is 9 local days long. Since the local day is 30 hours (from Zeb’s Guide), the week is 270 hours long. I want the orbital period of Kran to be something near this value so I just rolled four d10s to refine the number. The first one, I subtracted 5 from to get a number to add or subtract from 270, and the next 3 were just read as digits to represent the first 3 digits after the decimal place.
I rolled a 5 for the first die which meant no offset and then I got a 6, a 10(0), and a 4 so the orbital period of Kran is 270.604 hours. I realized later in the process that I should have probably given a bit more range the the +/- die but it’s fine as it is.
We’re also going to want to have a mass for the moon as that will have a small impact on its orbital distance. Since I wanted this moon to be small but still basically spherical, I just arbitrarily picked a size that was near to the size of the asteroid Ceres. I rolled some dice to pick exact values (although now I don’t remember exactly the rationale behind what I rolled) and came up with a value of 0.0125 times the mass of the Moon.
To get the size of the moon given its mass, we need its density. Referring back to the possible densities of the planets from the original article, I wanted to pick something in the 2-6 gm/cm3 range. So I rolled a d4+1 for the integer part and some d10s to get two decimal places and came up with
a density of 2.71 gm/cm3 for the moon.
Okay, now we’re all set to calculate the final values. Determining the radius is straightforward, we’re just back to this equation:
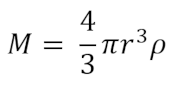
Only we’re solving for that r in there instead of M. That gives us a radius of 432.51 km. Next we want the orbital distance which takes us back to this equation:

where we are solving for a. M1 is the mass of the planet, and M2 is the mass of the moon. Again I used this handy website but since you can’t actually solve for a, I had to try various distances until I got the period to match. So it might have actually been faster to do the math on my calculator but oh well. We end up with a result of 198,336.5 km as the orbital distance for Kran.
For reference the diameter of Earth’s moon is 3474.2 km, almost exactly 8 times bigger, and it’s orbital distance is on average 384,400 km, so Kran is nearly twice as close.
Gluk & Clud
I’m not going to go over every detail of the other two moons but suffice it to say I followed the same procedure for each of those. The only constraints I had was that I wanted Gluk to be the largest of the three moons and have it’s orbital period correspond to between 1/8 to 1/14 of a year to represent the month concept. Clud was going to be way out there and orbit only about 4 times a year to correspond to the seasons.
After working through all the math we get the following results for each of the moons:
| Name | Orbital Period (hrs) | Orbital Distance (km) | Mass (moon) | Density (gm/cm3) | Radius (km) |
| Kran | 270.604 | 198,336.5 | 0.0125 | 2.71 | 432.5 |
| Gluk | 1,026.836 | 483,757.2 | 0.5237 | 3.14 | 1,430.2 |
| Clud | 2,826.842 | 948,883.7 | 0.2413 | 3.46 | 1,069.5 |
This image shows the sizes of the moons relative to each other and to Earth’s Moon. The image on the left shows their actual physical sizes if they were all side by side. The image on the right shows their apparent sizes as seen from the surface of Hum (assuming the Moon was dropped in at the proper distance).
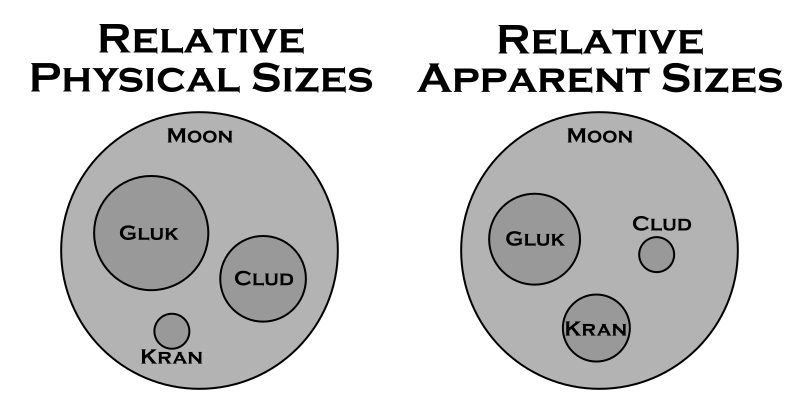
The moons are all physically smaller than the Earth’s moon by quite a bit and appear smaller in the sky. Also, notice that because Kran is so much closer than the other moons, although it is physically the smallest, it appears almost as big as Gluk and larger than Clud.
Hum’s Rotation Period
One more thing we need to establish is the actual rotation period of Hum. The information in Zeb’s Guide said it was 30 hours. However, I want to add a few more decimal places but still have it round to 30. So employing my usual method, I rolled d10-6 (to get a value between -5 and +4) and then two d10s for decimal places. I then added that to 30 to get the actual rotation period in hours. I ended up with 30.09 hours.
The Calendar
Now that we have all the physical data we need, we can get on to the actual purpose of this post, determining the calendar of the planet Hum.
Length of Year
The first thing to determine is the length of the year in local days. We have the orbital period of the planet (11,323.3 hours – about 30% longer than an earth year and 41.5% longer than the Frontiers’ Galactic Standard Year) and the rotation period of the planet (30.09 hours) so we just divide and find that the Hum year is 376.3144 local days long.
In local day terms, the year is only a bit longer than an Earth year, just 11 days more. It also tells us we’re going to need leap years, about every third year. We’ll come back to that.
In the previous sections, with the exception of the moon Kran, I sort of glossed over the relationship between the orbital periods of the moons as they relate to the length of the Hum year. Now let’s look at that in detail.
A Week on Hum
The inner moon Kran has an orbital period of 270.604 hours. Dividing this by the length of a day (30.09) hours, we get that Kran orbits every 8.993 days. That’s almost exactly 9 days. In fact, amazingly close to to exactly 9 days. Which is why I said above, I should have allowed for a bit more variation.
But that’s fine, sometimes you get lucky. So we’ll define a week on Hum to be 9 days long. At some point the start of first day of the week corresponds to the full Kran on the meridian but since the cycles slowly drift, that only occurs every once in a while and the phases slowly move through the week.
Comparing Kran’s orbital period to the year, we see that it makes 41.84 orbits each year so a typical year is almost 42 weeks long.
A Hum Month
If we compare the orbital period of the moon Gluk to the length of day we see that it’s orbital period corresponds to 34.125 days. And comparing it to the planet’s orbital period, it makes 11.02737 orbits in a single year.
Since I’m going to tie the concept of a month to the orbit of Gluck, a nominal month is 34 days long and there are 11 months in the year. There might be some variation like on Earth but this works as a base line.
With eleven 34-day months, that accounts for 374 of the 376.31 days of the year, leaving 2 extra days in the calendar. I’m going to assign one of those days to one of the months making it 35 days long (in the spring) and the other will be a holiday celebrating the passing/new year and will occur at the end of summer which will be when the Hum calendar year ends.
A Seasonal Moon
That leaves us with Clud. It’s orbit is 93.95 days long and it orbits 4.006 times each year, completing one orbit every season. Since the timing of its orbit doesn’t quite line up with the planet’s orbital period, the timing of the full phase of this moon slowly shifts (by just over half a day a year) over the centuries but the humma have tracked this for millennia and know the pattern.
Leap Years
All that’s left is to deal with that pesky 0.3144 days left over after each year. Multiplying by 3 gives us 0.943 days, which is just enough to be considered another day. Thus every third year, the end of year holiday is a two day event instead of a single day adding an extra day on that particular year but not part of any month.
It’s not quite a full day though and so every 51 years, the deviations add up enough that the extra day is not added to the calendar, just like on Earth when we don’t add in the leap day on years divisible by 100.
Finally, there is one more minor correction and that occurs every 1530 years. On that year, which would normally be a year the extra day is skipped, the extra day is included (just like including the leap day here on Earth in years that are divisible by 400 as occurred in the year 2000). This has only occurred once since this calendar was established and the next one won’t occur for another 172 years.
The Final Calendar
So the final Hum calendar looks like this:
- One week is 9 days long – in modern times it is a 6 day work week with a 3 day weekend
- Each year has 11 months plus one holiday at the end of the year to celebrate the harvest and ring in the new year. This feast day/beginning of the new year corresponds to the end of the Hum summer (what we would call fall)
- One month consists of 34 days, or nearly 4 weeks. The exception to this is the 5th month which is 35 days long. This occurs during the planting season giving one more day in that month.
- Every three years there is a leap day, extending the harvest holiday into a 2 day event instead of a single day.
- Except that every 51 years, the leap day is skipped and every 1530 years the day that would be skipped is included.
One more thing we need is to anchor this calendar with the Frontier standard calendar. To do that I’m going to say that the start of Hum year 2898 will coincide with FY60.124 and that year is a leap year so the end of year celebration (that starts on FY61.290) will last two days.
Last Thoughts
I realized as I was typing this up, that I didn’t account for the difference between sidereal and synodic periods for the moons. The orbital periods listed are really the synodic periods (as seen from the surface of Hum) but I treated them like the sidereal periods for computing orbital distances. Which means the distances are a bit off. The differences would be relatively small but that’s something I should revisit in the future. The rotation period for Hum is definitely the solar period (noon to noon) and not the sidereal period.
Otherwise, this is a pretty good description of Hum and its moons and a reasonable calendar for the system. I didn’t touch on Forge or Larg, the two other inhabited worlds in the Fochrik system. I’m assuming this calendar predates the humma’s space age and so is the foundation of any other calendar system on the other worlds. How it was adapted might be another article in the future but for now is left as an exercise for the reader.
What do you think of the calendar system presented? What would you have done differently? What do you like? Let me know in the comments below.



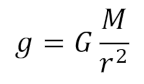

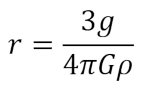
 ).
).